人口動態統計の死亡増の原因を探る⑦結論 [mespesado理論]
《計算結果の評価としては、「実際のワ〇チ〇死亡者は報告件数の少なくとも10倍以上である」という結論になり、この結論は、多くのワ〇チ〇に疑いを持つ人たちの主張する結果とほぼ同じレベルになっています。》
《よく反ワ○チ○界隈で、接種後死亡報告の数字がどの程度過小評価されているかについて、10倍どころか数十倍、あるいは100倍とか言っている人がいますが、私はそれは行きすぎだと思っています。・・・あまり数量的な根拠は無いですが、せいぜい10倍から15倍くらいの間じゃないかな、という気がしています。》
本格的な統計分析による結論です。感覚の裏付けとして実にありがたい。新たなデータが出た段階であらためて詳細な分析が行われるとのことです。今後どのように推移して行くのか、冷静な分析をさらに期待したいと思います。
* * * * *
510 名前:mespesado 2022/11/14 (Mon) 19:36:16
>>507
さて、50~54歳の「悪性新生物」と「心疾患」の超過死亡とワ〇チ〇後の死亡報告の件数から、この死亡報告がどれだけ過小評価されているのかを大胆に推計する方法を解説します。
まず以前にも書いたように、第④波の期間を4月~7月、第⑤波の期間を8月~12月と決めておきます。すると、それぞれの期間における「悪性新生物」を死因とする超過死亡率、「心疾患」を死因とする超過死亡率、そしてワ〇チ〇後の死亡の件数が計算できます。
ある期間において、超過死亡がE人、ワ〇チ〇後の死亡報告がW人だったとし、ここでワ〇チ〇死の報告が実際の死亡より過少報告されている、その過少報告率の逆数をMと置きます。ただしMは公表値からは不明で、これから方程式を解いて求めなければならない未知数です。つまり、ワ〇チ〇後の死亡報告がW人ですから、ワ〇チ〇後の本当の死亡者数は、WにMを乗じてW×M人となります。一方、超過死亡はE人ですから、このうちワ〇チ〇による死亡W×M人を差し引いたE-W×M人が新型コロナによる直接又は間接の超過死亡者数ということになります。
この数式を第④波に当てはめると、第④波の新型コロナによる直接又は間接の死亡者数は
[E4]-[W4]×[M4]
となります。ただし[E4]は第④波における超過死亡者数、[W4]は第④波におけるワ〇チ〇後の死亡報告件数、[M4]は第④波におけるワ〇チ〇後死の過少報告率の逆数です。同様にして、第⑤波の新型コロナによる直接又は間接の死亡者数は
[E5]-[W5]×[M5]
となります。ただし[E5]は第⑤波における超過死亡者数、[W5]は第⑤波におけるワ〇チ〇後の死亡報告件数、[M5]は第⑤波におけるワ〇チ〇後死の過少報告率の逆数です。
さて、ここで、>>496 の添付画像↓
https://bbs6.fc2.com//bbs/img/_409100/409098/full/409098_1667754029.png
で、全年齢合計で見たときの、第④波と第⑤波の超過死亡者数が、新型コロナの重症者数に比例していることを指摘しました。そして、死亡者や重症者の大半は高齢者であり、死亡者の中心である高齢者ではワ〇チ〇後の死者数は、他の死亡者の中に「埋もれ」てしまっていることも見てきました。このことから、一つの仮定として、
# どの年齢においても、「第⑤波での新型コロナによる直接又は間接死者
# 数」と「第④波での新型コロナによる直接又は間接死者数」の比は同じ
# である
と仮定してみることにします。この「比率」をαと書くと、αは、>>496 の添付画像で示したように、第⑤波における重症者数と第④波における重症者数の比に等しいので、
α=(第⑤波の重症者数)÷(第④波の重症者数)=112,960÷98,267=1.15
となります。以上の結果を50~54歳の第④波と第⑤波における新型コロナによる直接又は間接の死亡者数の場合に適用してみましょう。αは年齢に依らない定数だと仮定しましたから、
α=(50~54歳の第⑤波での新型コロナによる直接又は間接死者数)
÷(50~54歳の第④波での新型コロナによる直接又は間接死者数)
=([E5]-[W5]×[M5])÷([E4]-[W4]×[M4])
という等式が成り立つことになります。この数式の右辺の割り算の分母を払って変形すると、
[E5]-[W5]×[M5]=α×([E4]-[W4]×[M4])
という数式になります。ここで更に、ワ〇チ〇死亡報告の過少報告率も年齢に依らないと仮定することにします。すると、
[M5]=[M4]
となるので、この[M5]と[M4]を同じ変数Mで表せば、
[E5]-[W5]×M=α×([E4]-[W4]×M)
となります。これを更に括弧をほどいて
[E5]-[W5]×M=α×[E4]-α×[W4]×M
と変形し、更に移項して
[E5]-α×[E4]=[W5]×M-α×[W4]×M
としてからMについてまとめると、
[E5]-α×[E4]=([W5]-α×[W4])×M
となるので、未知数だったM(=死亡報告の過少報告率の逆数)は、
M=([E5]-α×[E4])÷([W5]-α×[W4])
という形に求められることになります。
ここで、50~54歳の場合について、[E5]、[E4]、[W5]、[W4]にそれぞれ実際の数字を代入して死亡報告の過少報告率の逆数Mを求めてみましょう。
[E5]=339
[E4]=134
[W5]=19
[W4]=4
一方、
α=1.15
でしたから、上の式にこれらの数値を代入すれば、
M=(339-1.15×134)÷(19-1.15×4)=12.8
となり、これは「ワ〇チ〇死亡の報告件数は、12.8分の1に過少報告されている」という結論になります。
ただ、全死因に対する超過死亡だと、例えば「自殺」のような、直接新型コロナの感染率とも連動しないけれども無関係ではない複雑な関係があるような死因によるものが含まれてしまいますから、上記の計算の前提がそもそも崩れてしまいます。そこで、>>507 で炙り出した「超過死亡が第④波でほとんどゼロ、第⑤波で顕著に増加した死因」の場合に限定して上の計算を行ってみることにします。この場合は
[E5]=(悪性新生物の超過死亡)+(心疾患の超過死亡)=86+74=160
[E4]=(悪性新生物の超過死亡)+(心疾患の超過死亡)=△2+18=16
[W5]=19
[W4]=4
となるので
M=(160-1.15×16)÷(19-1.15×4)=9.8
となり、全死因で計算した値とほぼ同じ数値が得られます。ただし、この計算の分母は、悪性新生物や心疾患以外でのワ〇チ〇後死亡を含んでいるので過大評価されている可能性が高いので、その過大評価された数値で割り算して求めたMは過小評価されている可能性が高い。ですから、この計算結果の評価としては、「実際のワ〇チ〇死亡者は報告件数の少なくとも10倍以上である」という結論になり、この結論は、多くのワ〇チ〇に疑いを持つ人たちの主張する結果とほぼ同じレベルになっています。 (続く)
513 名前:mespesado 2022/11/15 (Tue) 10:39:14
https://bbs6.fc2.com//bbs/img/_409100/409098/full/409098_1668476354.png
>>510
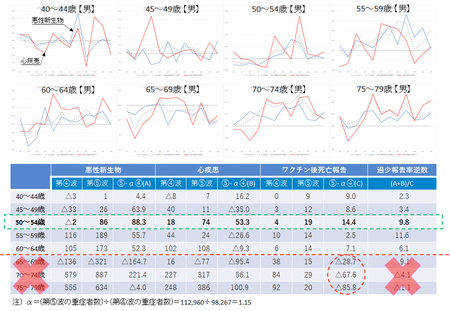
男性50~54歳の「悪性新生物」と「心疾患」によるワ〇チ〇後死亡報告の過少報告率の推理を他の年齢層についても行ってみたのが添付画像です。
一応40歳~79歳まで、もとの50~54歳を含めて8通りを計算してみましたが、上段のグラフで見ると、悪性新生物の青線グラフと全死因の破線グラフがほぼ同傾向にあるのに対し、心疾患のグラフはそれらとはかなり違う動きをしています。そして、過少報告率の逆数Mの値(下段の表の一番右の欄)を見ると、55~59歳の欄も11.6と、約10倍になっていて、もとの50~54歳と近い値になっていますが、内訳をよく見ると、心疾患の「⑤-α④(B)」の欄がマイナスになっている!これはつまり、悪性新生物と心疾患を併せ考えるとプラスになっているが、その一要素である心疾患だけだとそうなっていないというわけで、これは「自殺」ほどではないけれど、新型コロナ感染者数に比例はしないけれど、かといって独立ではない動きをする一部の死因がこれらの中に紛れ込んでいるということを意味するのかも知れません。そして、50代を離れると、過少報告率逆数は10からどんどん離れて行き、65歳以上の年齢層では、過少報告率逆数だけでなく、分母の「⑤-α④(C)」の欄すらマイナスになってしまっています。ところがこれは不思議でも何でもなく、ワ〇チ〇接種が65歳未満と65歳以上で時期が分けられていて、実際に65歳未満ではその時期が第⑤波と重なっていたけれど、65歳以上では第④波と第⑤波のはざまの7月頃に重なっていたため、データを第④波と第⑤波に分けてそこから計算を行うことが、65歳以上では不適切になってしまっているわけです。添付画像下段のグラフの65歳以上(バッテンを付けた部分)の不規則性はその事実の反映でしょう。
では65歳以上の年齢層で、この過少報告率逆数を計算する別の方法は何かないものでしょうか。次はその一方法について考えてみることにします。 (続く)
515 名前:mespesado 2022/11/15 (Tue) 15:24:48
https://bbs6.fc2.com//bbs/img/_409100/409098/full/409098_1668493488.png
>>513
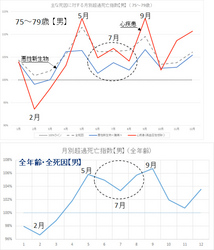
前発言 >>513 の添付画像から75~79歳のグラフを抜き出してきたのが本発言の添付画像の上段のグラフです。これ、すごく特徴的な部分がある。それは点線の丸で囲んだ7月のところです。比較のために、>>492 で貼り付けた画像の男性の全年齢・全死因による超過死亡のグラフを下段に再掲してみました。7月前後の部分を比較してみれば明らかなように、下段のグラフでは7月が第④波と第⑤波のはざまで完全な谷になっているのに対し、上段のグラフでは7月だけぴょこんと小さな山になっている。この時期は新型コロナの流行の谷間であると同時に65歳以上のワ○チ○接種のピークがあった月なので、その原因はあまりにもはっきりしていると思います。そこで、この75~79歳のグラフの元データを使って、この7月のワ○チ○による実際の死亡者数を定量的に推計してみることにしましょう。
まず、75~79歳の6月の超過死亡者数を[A6]、7月と8月のそれを、それぞれ[A7]、[A8]とします。
次に、全年齢・全死因の6月の超過死亡者数を[B6]、7月と8月のそれを、それぞれ[B7]、[B8]とします。
また、ワ〇チ〇後の6月の死亡報告者数を[W6]、7月と8月のそれを、それぞれ[W7]、[W8]とします。
最後にワ〇チ〇死の報告が実際の死亡より過少報告されている、その過少報告率の逆数を前と同様にMと置きます。ここでもMは公表値からは不明で、これから方程式を解いて求めなければならない未知数です。
さて、このとき6月の超過死亡者数 [A6] からワ○チ○で実際に死亡した人数である M×[W6] を差し引いた残り、つまり
[A6]-M×[W6]
が6月に新型コロナによる直接又は間接的に死亡した人数になるはずです。
同様に、7月の新型コロナによる直接又は間接的に死亡した人数は
[A7]-M×[W7]
であり、8月の新型コロナによる直接又は間接的に死亡した人数は
[A8]-M×[W8]
ということになります。ここで、7月がどれだけ前後に比べて出っ張っているかという「尖度」を、「7月の値を6月と8月の値の平均値で割ったもの」で定義します(注:この尖度というのはここだけの便宜的な用語で、統計学の術語としての尖度とは別物です)。7月が6月と8月の丁度平均値である、つまり、6―7―8月が真っ平になった場合の「尖度」が1ということになり、尖度が1を超えると7月が山になり、尖度が1を下回ると7月が谷になる、ということを意味します。
具体的に、まずは簡単な「全年齢・全死因の超過死亡」に関する尖度の方から計算してみることにします。7月の値が [B7] で、6月と8月の平均値が ([B6]+[B8])÷2 ですから、この場合の尖度(P1とします)は
P1=[B7]÷{([B6]+[B8])÷2}
=2×[B7]÷([B6]+[B8])
となります。
次に、新型コロナによる直接又は間接的に死亡した人数の尖度(P2)を求めます。これは、P1の計算で[B6]とあるところを[A6]-M×[W6]に、[B7]を[A7]-M×[W7]に、[B8]を[A8]-M×[W8]に置き換えればよいので、
P2=2×([A7]-M×[W7])÷([A6]-M×[W6]+[A8]-M×[W8])
となります。ここで、>>510 のときと同様に、死亡者の大半は高齢者であり、死亡者の中心である80代以上の高齢者ではワ〇チ〇後の死者数は、他の死亡者の中に「埋もれ」てしまっていることに注目して、次のような仮定を導入することにします:
# 75~79歳の新型コロナによる直接又は間接死亡者数に関する「尖度」
# は、全年齢・全死因に対する超過死亡に関する「尖度」と同じである。
つまり、新型コロナによる死亡の月別の変動は年齢によらず一定で、特定の年齢層のグラフの尖度を変化させている原因はワ○チ○種だ、と仮定する、ということです。この仮定の下では
P1=P2
ということですから、未知数Mに対する方程式として
2×[B7]÷([B6]+[B8])
=2×([A7]-M×[W7])÷([A6]-M×[W6]+[A8]-M×[W8])
という式が得られます。これを(分数と見做して)分母を払って変形すると、
([A7]-M×[W7])×([B6]+[B8])
=[B7]×([A6]-M×[W6]+[A8]-M×[W8])
となりますが、両辺を [B7]で割って、
β=([B6]+[B8])÷[B7]
と置くと、
β×([A7]-M×[W7])=[A6]-M×[W6]+[A8]-M×[W8]
左辺の括弧をほどいて移項すると
β×[A7]-[A6]-[A8]=M×β×[W7]-M×[W6]-M×[W8]
右辺をMでまとめると、
β×[A7]-[A6]-[A8]=M×(β×[W7]-[W6]-[W8])
となり、未知数だったMは、
M=(β×[A7]-[A6]-[A8])÷(β×[W7]-[W6]-[W8])
と計算できることになります。
以下、具体的にMを計算してみます。まず全年齢・全死因のデータからβを求めます。全年齢・全死因の超過死亡のグラフの元データによれば、
[B6]=4.94%
[B7]=3.37%
[B8]=5.72%
ですから、
β=([B6]+[B8])÷[B7]=(4.94+5.72)÷3.37=3.16
となります。また
[A6]=441
[A7]=467
[A8]=505
[W6]=48
[W7]=31
[W8]=12
ですから、求めるべき報告過少率の逆数 M は、
M=(β×[A7]-[A6]-[A8])÷(β×[W7]-[W6]-[W8])
=(3.16×467-441-505)÷(3.16×31-48-12)
=14.0
と求められます。これも6~8月の超過死亡数 [A6],[A7],[A8] に全死因の数字を使っていますが、そこには「自殺」のような、感染数に連動しないけれども無関係とは言えないような微妙な死因が含まれています。
そこで、前回と同様に、全死因の代わりに「悪性新生物」と「心疾患」に死因を限定した場合を考えると、
[A6]= 45+38= 83
[A7]=120+58=178
[A8]= 69+36=105
となるので、上のMの計算式で対応する箇所を置き換えて再計算すると、
M=(β×[A7]-[A6]-[A8])÷(β×[W7]-[W6]-[W8])
=(3.16×178-83-105)÷(3.16×31-48-12)
=9.9
となり、何と、今回の計算方法でも約10倍という結果が得られました!
あまりにも出来過ぎた結果にも思えますが、これで65歳未満だけでなく、65歳以上の年齢層においてもワ○チ○による実際の死亡者数は、死亡報告の10倍程度の人数であることがわかったと思います。
以上で2021年の超過死亡に関する分析は一応終わりたいと思います。人口動態統計では、今年2022年に入ってからも、2~3月や8月の超過死亡が半端なく大きく、巷でも話題になっていますが、死因も含む統計が、現時点では7月分までしか公表されていませんので、8月分まで公表された段階で、改めて分析してみたいと思っています。その時は、改めて「復活宣言」して分析結果をまたシリーズもので解説したいと思うので、その節はどうぞよろしくお願い致します。 (一応おしまい)
>>507
さて、50~54歳の「悪性新生物」と「心疾患」の超過死亡とワ〇チ〇後の死亡報告の件数から、この死亡報告がどれだけ過小評価されているのかを大胆に推計する方法を解説します。
まず以前にも書いたように、第④波の期間を4月~7月、第⑤波の期間を8月~12月と決めておきます。すると、それぞれの期間における「悪性新生物」を死因とする超過死亡率、「心疾患」を死因とする超過死亡率、そしてワ〇チ〇後の死亡の件数が計算できます。
ある期間において、超過死亡がE人、ワ〇チ〇後の死亡報告がW人だったとし、ここでワ〇チ〇死の報告が実際の死亡より過少報告されている、その過少報告率の逆数をMと置きます。ただしMは公表値からは不明で、これから方程式を解いて求めなければならない未知数です。つまり、ワ〇チ〇後の死亡報告がW人ですから、ワ〇チ〇後の本当の死亡者数は、WにMを乗じてW×M人となります。一方、超過死亡はE人ですから、このうちワ〇チ〇による死亡W×M人を差し引いたE-W×M人が新型コロナによる直接又は間接の超過死亡者数ということになります。
この数式を第④波に当てはめると、第④波の新型コロナによる直接又は間接の死亡者数は
[E4]-[W4]×[M4]
となります。ただし[E4]は第④波における超過死亡者数、[W4]は第④波におけるワ〇チ〇後の死亡報告件数、[M4]は第④波におけるワ〇チ〇後死の過少報告率の逆数です。同様にして、第⑤波の新型コロナによる直接又は間接の死亡者数は
[E5]-[W5]×[M5]
となります。ただし[E5]は第⑤波における超過死亡者数、[W5]は第⑤波におけるワ〇チ〇後の死亡報告件数、[M5]は第⑤波におけるワ〇チ〇後死の過少報告率の逆数です。
さて、ここで、>>496 の添付画像↓
https://bbs6.fc2.com//bbs/img/_409100/409098/full/409098_1667754029.png
で、全年齢合計で見たときの、第④波と第⑤波の超過死亡者数が、新型コロナの重症者数に比例していることを指摘しました。そして、死亡者や重症者の大半は高齢者であり、死亡者の中心である高齢者ではワ〇チ〇後の死者数は、他の死亡者の中に「埋もれ」てしまっていることも見てきました。このことから、一つの仮定として、
# どの年齢においても、「第⑤波での新型コロナによる直接又は間接死者
# 数」と「第④波での新型コロナによる直接又は間接死者数」の比は同じ
# である
と仮定してみることにします。この「比率」をαと書くと、αは、>>496 の添付画像で示したように、第⑤波における重症者数と第④波における重症者数の比に等しいので、
α=(第⑤波の重症者数)÷(第④波の重症者数)=112,960÷98,267=1.15
となります。以上の結果を50~54歳の第④波と第⑤波における新型コロナによる直接又は間接の死亡者数の場合に適用してみましょう。αは年齢に依らない定数だと仮定しましたから、
α=(50~54歳の第⑤波での新型コロナによる直接又は間接死者数)
÷(50~54歳の第④波での新型コロナによる直接又は間接死者数)
=([E5]-[W5]×[M5])÷([E4]-[W4]×[M4])
という等式が成り立つことになります。この数式の右辺の割り算の分母を払って変形すると、
[E5]-[W5]×[M5]=α×([E4]-[W4]×[M4])
という数式になります。ここで更に、ワ〇チ〇死亡報告の過少報告率も年齢に依らないと仮定することにします。すると、
[M5]=[M4]
となるので、この[M5]と[M4]を同じ変数Mで表せば、
[E5]-[W5]×M=α×([E4]-[W4]×M)
となります。これを更に括弧をほどいて
[E5]-[W5]×M=α×[E4]-α×[W4]×M
と変形し、更に移項して
[E5]-α×[E4]=[W5]×M-α×[W4]×M
としてからMについてまとめると、
[E5]-α×[E4]=([W5]-α×[W4])×M
となるので、未知数だったM(=死亡報告の過少報告率の逆数)は、
M=([E5]-α×[E4])÷([W5]-α×[W4])
という形に求められることになります。
ここで、50~54歳の場合について、[E5]、[E4]、[W5]、[W4]にそれぞれ実際の数字を代入して死亡報告の過少報告率の逆数Mを求めてみましょう。
[E5]=339
[E4]=134
[W5]=19
[W4]=4
一方、
α=1.15
でしたから、上の式にこれらの数値を代入すれば、
M=(339-1.15×134)÷(19-1.15×4)=12.8
となり、これは「ワ〇チ〇死亡の報告件数は、12.8分の1に過少報告されている」という結論になります。
ただ、全死因に対する超過死亡だと、例えば「自殺」のような、直接新型コロナの感染率とも連動しないけれども無関係ではない複雑な関係があるような死因によるものが含まれてしまいますから、上記の計算の前提がそもそも崩れてしまいます。そこで、>>507 で炙り出した「超過死亡が第④波でほとんどゼロ、第⑤波で顕著に増加した死因」の場合に限定して上の計算を行ってみることにします。この場合は
[E5]=(悪性新生物の超過死亡)+(心疾患の超過死亡)=86+74=160
[E4]=(悪性新生物の超過死亡)+(心疾患の超過死亡)=△2+18=16
[W5]=19
[W4]=4
となるので
M=(160-1.15×16)÷(19-1.15×4)=9.8
となり、全死因で計算した値とほぼ同じ数値が得られます。ただし、この計算の分母は、悪性新生物や心疾患以外でのワ〇チ〇後死亡を含んでいるので過大評価されている可能性が高いので、その過大評価された数値で割り算して求めたMは過小評価されている可能性が高い。ですから、この計算結果の評価としては、「実際のワ〇チ〇死亡者は報告件数の少なくとも10倍以上である」という結論になり、この結論は、多くのワ〇チ〇に疑いを持つ人たちの主張する結果とほぼ同じレベルになっています。 (続く)
513 名前:mespesado 2022/11/15 (Tue) 10:39:14
https://bbs6.fc2.com//bbs/img/_409100/409098/full/409098_1668476354.png

>>510
男性50~54歳の「悪性新生物」と「心疾患」によるワ〇チ〇後死亡報告の過少報告率の推理を他の年齢層についても行ってみたのが添付画像です。
一応40歳~79歳まで、もとの50~54歳を含めて8通りを計算してみましたが、上段のグラフで見ると、悪性新生物の青線グラフと全死因の破線グラフがほぼ同傾向にあるのに対し、心疾患のグラフはそれらとはかなり違う動きをしています。そして、過少報告率の逆数Mの値(下段の表の一番右の欄)を見ると、55~59歳の欄も11.6と、約10倍になっていて、もとの50~54歳と近い値になっていますが、内訳をよく見ると、心疾患の「⑤-α④(B)」の欄がマイナスになっている!これはつまり、悪性新生物と心疾患を併せ考えるとプラスになっているが、その一要素である心疾患だけだとそうなっていないというわけで、これは「自殺」ほどではないけれど、新型コロナ感染者数に比例はしないけれど、かといって独立ではない動きをする一部の死因がこれらの中に紛れ込んでいるということを意味するのかも知れません。そして、50代を離れると、過少報告率逆数は10からどんどん離れて行き、65歳以上の年齢層では、過少報告率逆数だけでなく、分母の「⑤-α④(C)」の欄すらマイナスになってしまっています。ところがこれは不思議でも何でもなく、ワ〇チ〇接種が65歳未満と65歳以上で時期が分けられていて、実際に65歳未満ではその時期が第⑤波と重なっていたけれど、65歳以上では第④波と第⑤波のはざまの7月頃に重なっていたため、データを第④波と第⑤波に分けてそこから計算を行うことが、65歳以上では不適切になってしまっているわけです。添付画像下段のグラフの65歳以上(バッテンを付けた部分)の不規則性はその事実の反映でしょう。
では65歳以上の年齢層で、この過少報告率逆数を計算する別の方法は何かないものでしょうか。次はその一方法について考えてみることにします。 (続く)
515 名前:mespesado 2022/11/15 (Tue) 15:24:48
https://bbs6.fc2.com//bbs/img/_409100/409098/full/409098_1668493488.png

>>513
前発言 >>513 の添付画像から75~79歳のグラフを抜き出してきたのが本発言の添付画像の上段のグラフです。これ、すごく特徴的な部分がある。それは点線の丸で囲んだ7月のところです。比較のために、>>492 で貼り付けた画像の男性の全年齢・全死因による超過死亡のグラフを下段に再掲してみました。7月前後の部分を比較してみれば明らかなように、下段のグラフでは7月が第④波と第⑤波のはざまで完全な谷になっているのに対し、上段のグラフでは7月だけぴょこんと小さな山になっている。この時期は新型コロナの流行の谷間であると同時に65歳以上のワ○チ○接種のピークがあった月なので、その原因はあまりにもはっきりしていると思います。そこで、この75~79歳のグラフの元データを使って、この7月のワ○チ○による実際の死亡者数を定量的に推計してみることにしましょう。
まず、75~79歳の6月の超過死亡者数を[A6]、7月と8月のそれを、それぞれ[A7]、[A8]とします。
次に、全年齢・全死因の6月の超過死亡者数を[B6]、7月と8月のそれを、それぞれ[B7]、[B8]とします。
また、ワ〇チ〇後の6月の死亡報告者数を[W6]、7月と8月のそれを、それぞれ[W7]、[W8]とします。
最後にワ〇チ〇死の報告が実際の死亡より過少報告されている、その過少報告率の逆数を前と同様にMと置きます。ここでもMは公表値からは不明で、これから方程式を解いて求めなければならない未知数です。
さて、このとき6月の超過死亡者数 [A6] からワ○チ○で実際に死亡した人数である M×[W6] を差し引いた残り、つまり
[A6]-M×[W6]
が6月に新型コロナによる直接又は間接的に死亡した人数になるはずです。
同様に、7月の新型コロナによる直接又は間接的に死亡した人数は
[A7]-M×[W7]
であり、8月の新型コロナによる直接又は間接的に死亡した人数は
[A8]-M×[W8]
ということになります。ここで、7月がどれだけ前後に比べて出っ張っているかという「尖度」を、「7月の値を6月と8月の値の平均値で割ったもの」で定義します(注:この尖度というのはここだけの便宜的な用語で、統計学の術語としての尖度とは別物です)。7月が6月と8月の丁度平均値である、つまり、6―7―8月が真っ平になった場合の「尖度」が1ということになり、尖度が1を超えると7月が山になり、尖度が1を下回ると7月が谷になる、ということを意味します。
具体的に、まずは簡単な「全年齢・全死因の超過死亡」に関する尖度の方から計算してみることにします。7月の値が [B7] で、6月と8月の平均値が ([B6]+[B8])÷2 ですから、この場合の尖度(P1とします)は
P1=[B7]÷{([B6]+[B8])÷2}
=2×[B7]÷([B6]+[B8])
となります。
次に、新型コロナによる直接又は間接的に死亡した人数の尖度(P2)を求めます。これは、P1の計算で[B6]とあるところを[A6]-M×[W6]に、[B7]を[A7]-M×[W7]に、[B8]を[A8]-M×[W8]に置き換えればよいので、
P2=2×([A7]-M×[W7])÷([A6]-M×[W6]+[A8]-M×[W8])
となります。ここで、>>510 のときと同様に、死亡者の大半は高齢者であり、死亡者の中心である80代以上の高齢者ではワ〇チ〇後の死者数は、他の死亡者の中に「埋もれ」てしまっていることに注目して、次のような仮定を導入することにします:
# 75~79歳の新型コロナによる直接又は間接死亡者数に関する「尖度」
# は、全年齢・全死因に対する超過死亡に関する「尖度」と同じである。
つまり、新型コロナによる死亡の月別の変動は年齢によらず一定で、特定の年齢層のグラフの尖度を変化させている原因はワ○チ○種だ、と仮定する、ということです。この仮定の下では
P1=P2
ということですから、未知数Mに対する方程式として
2×[B7]÷([B6]+[B8])
=2×([A7]-M×[W7])÷([A6]-M×[W6]+[A8]-M×[W8])
という式が得られます。これを(分数と見做して)分母を払って変形すると、
([A7]-M×[W7])×([B6]+[B8])
=[B7]×([A6]-M×[W6]+[A8]-M×[W8])
となりますが、両辺を [B7]で割って、
β=([B6]+[B8])÷[B7]
と置くと、
β×([A7]-M×[W7])=[A6]-M×[W6]+[A8]-M×[W8]
左辺の括弧をほどいて移項すると
β×[A7]-[A6]-[A8]=M×β×[W7]-M×[W6]-M×[W8]
右辺をMでまとめると、
β×[A7]-[A6]-[A8]=M×(β×[W7]-[W6]-[W8])
となり、未知数だったMは、
M=(β×[A7]-[A6]-[A8])÷(β×[W7]-[W6]-[W8])
と計算できることになります。
以下、具体的にMを計算してみます。まず全年齢・全死因のデータからβを求めます。全年齢・全死因の超過死亡のグラフの元データによれば、
[B6]=4.94%
[B7]=3.37%
[B8]=5.72%
ですから、
β=([B6]+[B8])÷[B7]=(4.94+5.72)÷3.37=3.16
となります。また
[A6]=441
[A7]=467
[A8]=505
[W6]=48
[W7]=31
[W8]=12
ですから、求めるべき報告過少率の逆数 M は、
M=(β×[A7]-[A6]-[A8])÷(β×[W7]-[W6]-[W8])
=(3.16×467-441-505)÷(3.16×31-48-12)
=14.0
と求められます。これも6~8月の超過死亡数 [A6],[A7],[A8] に全死因の数字を使っていますが、そこには「自殺」のような、感染数に連動しないけれども無関係とは言えないような微妙な死因が含まれています。
そこで、前回と同様に、全死因の代わりに「悪性新生物」と「心疾患」に死因を限定した場合を考えると、
[A6]= 45+38= 83
[A7]=120+58=178
[A8]= 69+36=105
となるので、上のMの計算式で対応する箇所を置き換えて再計算すると、
M=(β×[A7]-[A6]-[A8])÷(β×[W7]-[W6]-[W8])
=(3.16×178-83-105)÷(3.16×31-48-12)
=9.9
となり、何と、今回の計算方法でも約10倍という結果が得られました!
あまりにも出来過ぎた結果にも思えますが、これで65歳未満だけでなく、65歳以上の年齢層においてもワ○チ○による実際の死亡者数は、死亡報告の10倍程度の人数であることがわかったと思います。
以上で2021年の超過死亡に関する分析は一応終わりたいと思います。人口動態統計では、今年2022年に入ってからも、2~3月や8月の超過死亡が半端なく大きく、巷でも話題になっていますが、死因も含む統計が、現時点では7月分までしか公表されていませんので、8月分まで公表された段階で、改めて分析してみたいと思っています。その時は、改めて「復活宣言」して分析結果をまたシリーズもので解説したいと思うので、その節はどうぞよろしくお願い致します。 (一応おしまい)
516 名前:mespesado 2022/11/15 (Tue) 17:50:48
>>515
ちょっと補足というか、おまけです。
よく反ワ○チ○界隈で、接種後死亡報告の数字がどの程度過小評価されているかについて、10倍どころか数十倍、あるいは100倍とか言っている人がいますが、私はそれは行きすぎだと思っています。なぜかというと、そもそも今回の連載の最初の方で、死亡率で見た場合で、しかも1~3月のインフルが消失した影響を除外した場合の超過死亡率は4%程度だということを確かめました。一方、日本人の1年間の死亡者数は約130万人ですから、超過死亡者数は、この130万人の4%、すなわち5万2千人程度ということになり、この中に新型コロナそのものによる直接又は間接死亡とワ○チ○死亡が含まれているわけですから、ワ○チ○死亡が5万2千人を超えることはありえません。ワ○チ○後の死亡報告が、私の統計ではP社のみの分なので、約千件であり、従って過少報告率の逆数は最大でも5万2千÷千、すなわち52倍にしかなりません。しかも80歳以上ではワ○チ○死は他の死者の中に「埋もれて」しまっているわけですから、この5万2千人の半分を超えていることは考えにくい。つまり26倍が限度で、それでも大きすぎるように思われます。ですから、これ以上はあまり数量的な根拠は無いですが、せいぜい10倍から15倍くらいの間じゃないかな、という気がしています。
>>515
ちょっと補足というか、おまけです。
よく反ワ○チ○界隈で、接種後死亡報告の数字がどの程度過小評価されているかについて、10倍どころか数十倍、あるいは100倍とか言っている人がいますが、私はそれは行きすぎだと思っています。なぜかというと、そもそも今回の連載の最初の方で、死亡率で見た場合で、しかも1~3月のインフルが消失した影響を除外した場合の超過死亡率は4%程度だということを確かめました。一方、日本人の1年間の死亡者数は約130万人ですから、超過死亡者数は、この130万人の4%、すなわち5万2千人程度ということになり、この中に新型コロナそのものによる直接又は間接死亡とワ○チ○死亡が含まれているわけですから、ワ○チ○死亡が5万2千人を超えることはありえません。ワ○チ○後の死亡報告が、私の統計ではP社のみの分なので、約千件であり、従って過少報告率の逆数は最大でも5万2千÷千、すなわち52倍にしかなりません。しかも80歳以上ではワ○チ○死は他の死者の中に「埋もれて」しまっているわけですから、この5万2千人の半分を超えていることは考えにくい。つまり26倍が限度で、それでも大きすぎるように思われます。ですから、これ以上はあまり数量的な根拠は無いですが、せいぜい10倍から15倍くらいの間じゃないかな、という気がしています。




コメント 0